
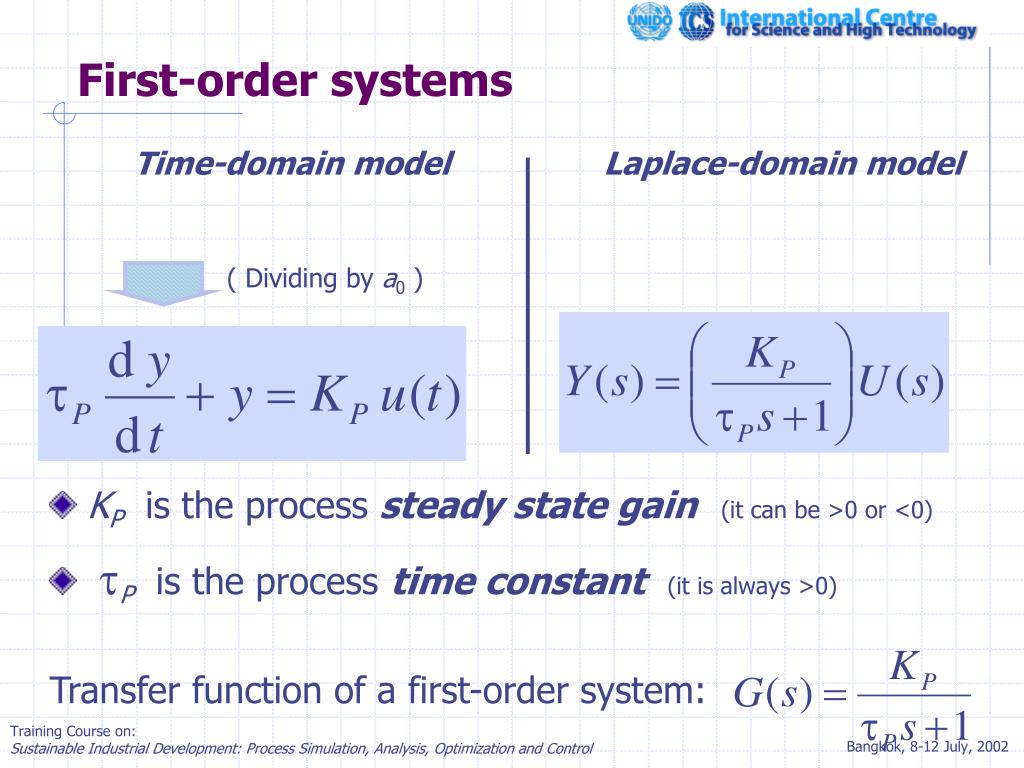
In order to determine the transfer function of any network or system, the steps are as follows: Procedure to calculate the transfer function of the Control System Whenever the frequency component of the transfer function i.e., ‘s’ is substituted as 0 in the transfer function of the system, then the achieved value is known as dc gain. Then such a plot is known as a pole-zero plot of the system. When all the poles and zeros of the transfer function are represented in the s-plane. It is basically the maximum power of s which is present in the characteristic equation (i.e., in the denominator polynomial). The order of the transfer function is defined by the characteristic equation of the system. The characteristic equation will be given as: The denominator of the transfer function of the system, when equated to 0, provides the characteristic equation of that particular system. Characteristic Equation of Transfer Function.These are the zeros of the transfer function, as these values on substitution make the overall transfer function of the system 0. The zeros can also be of 3 types depending upon, whether they are repetitive, non-repetitive or complex conjugate pairs.Ĭonsider that a system has a transfer function: Like the poles, the zeros are also roots of the equation, which is achieved when the term in the numerator is equated to 0. Those values of the s that when substituted in the numerator of the transfer function make the transfer function zero, is known as zeros of that transfer function. However, the zeros of the transfer function are evaluated using the numerator. We have already discussed that poles are specified by the denominator of the transfer function. The x-axis in the s-plane represents the poles. Whereas when there exist complex conjugate values of the poles then it is known as complex conjugate poles. While when the values of the poles are repetitive then such poles are known as repeated poles. If the values are real and non-repetitive, then such poles are known as simple poles. The poles of a transfer function generally are of three types: simple, repeated and conjugate poles. As the substitution of these values in the denominator leads to provide infinite transfer function. These are the poles of the above transfer function. Let we have a system with transfer function: When the term in the denominator is equated to zero then the obtained roots are known as poles. So, in the above equation, if s is substituted as s 1, s 2 - s n in the denominator, then these values act as the poles of the transfer function. Poles of the transfer function are defined as those values of the parameter ‘s’ whose substitution in the denominator makes the transfer function as infinite. In the factorized form the above equation can be written as: And so is represented as the ratio of polynomials in ‘s’. Terms related to the Transfer Function of a SystemĪs we know that transfer function is given as the Laplace transform of output and input. This is so because the feedback loop gets introduced in a closed-loop system. The open-loop and the closed-loop system have a different transfer function. Thus we can say that it is a mathematical function explaining the system parameters according to the applied input so as to get the desired output.


 0 kommentar(er)
0 kommentar(er)
